Informação, biologia e evolução Parte II
Continuamos a série de posts sobre informação, biologia e evolução iniciada no post Informação, biologia e evolução: Parte I.
A Teoria Molecular da Informação de Shannon:
Apesar do rigor matemático deste campo, muitos dos profissionais que trabalham com a Teoria da Informação* de Shannon, começando pelo próprio Shannon, nem sempre empregam os vários termos da teoria de maneira muito cuidadosa e, por vezes, o fazem de maneira ambígua. Como nosso interesse é compreender as aplicações da teoria de Shannon na biologia molecular e na biologia evolutiva, daqui em diante, seguirei a terminologia de um dos pesquisadores que está entre os principais responsáveis pela aplicação exitosa das ideias de Shannon à biologia molecular e a evolução, Thomas D. Schneider, do NCI/NIH. Também seguirei as definições e explicações de Schneider porque ele parece empregar a terminologia da maneira mais coerente, inclusive preservando as noções intuitivas sobre o que é informação e o que consistiria em um ganho desta mesma quantidade, o que é essencial para que consigamos compreender seu papel na evolução dos sistemas biológicos, pelo menos, ao nível molecular. Com este intuito farei uso extenso das explicações e exemplos contidos no tutorial [1] criado por Schneider e disponível em sua página, adicionando algumas informações e explicações retiradas de outras fontes, além de fazer alguns comentários, quando julgá-los pertinentes.
Informação e Incerteza:
Talvez a maior causa de confusão seja a equiparação dos termos 'informação', 'incerteza' e 'entropia' (informacional) que está presente em muitas das apresentações (inclusive técnicas) da teoria da informação e suas aplicações. A própria literatura da área, como explica Schneider, nos fornece vários exemplos disso. De acordo com o pesquisador, a principal razão para esta equiparação foi dada por Tribus (citado por Schneider) ao relatar a história clássica de que Shannon, ao não saber como chamar a sua medida (H(x)), aceitou a sugestão do famoso matemático austro-húngaro John von Neumann:
'Você deveria chamá-lo de entropia ... [pois] ... ninguém sabe o que realmente é a entropia, assim, em um debate, você sempre terá a vantagem' (Tribus, 1971 citado por Schneider) [1].
Shannon também referia-se a sua medida não só como 'entropia', mas também como 'incerteza', que, aliás, é a forma preferida por Schneider e que também adotarei neste post, principalmente, porque não se tem a incerteza unidades físicas a ela associada, como é o caso da entropia (devido a termodinâmica). Schneider é bem enfático ao apontar os perigos de equipararmos informação à incerteza. Caso não prestemos atenção para a diferença entre entropia/incerteza, de um lado, e informação, de outro, podemos acabar chegando a conclusão que a 'informação' é equivalente a aleatoriedade em sistemas físicos, tornando as coisas ainda mais confusas do que elas já são. Embora obviamente haja relação entre informação e incerteza, já que ambas podem ser usadas para descrever qualquer processo em que há a seleção de um ou mais estados ou objetos de um conjunto maior de objetos [1], devemos ter em mente que, ainda assim, existem diferenças fundamentais entre ambas. Mais adiante comentarei mais sobre isso, mas já fica aqui o alerta.
Mas afinal o que é informação?
A explicação de Schneider começa com ele pedindo ao leitor que suponha que exista um dispositivo que produza três símbolos diferentes, A, B ou C. Até que a máquina produza o próximo símbolo, não temos certeza de qual ele será, mas assim que o símbolo é produzido e nós o vemos, a nossa incerteza é diminuída e com isso podemos sinalizar que recebemos alguma informação. Este ponto é muito importante e deixa clara qual a relação entre informação e incerteza. Portanto, sem muita enrolação:
"A informação é a diminuição da incerteza."
Para quantificarmos a informação, então, precisamos medir a incerteza. A maneira mais simples de fazer isso é simplesmente dizermos que temos um grau de incerteza de “3 de símbolos", já que são três símbolos possíveis e não sabemos quais deles serão produzidos. Porém, isso começa a ficar mais complicado ao imaginarmos que exista um segundo dispositivo. Esse dispositivo porém produz os símbolos 1 e 2. Caso usássemos a mesma estratégia anterior diríamos que o segundo dispositivo tem um grau de incerteza de “2 símbolos". O problema de verdade surge ao combinarmos os dois dispositivos. Como existem seis possibilidades (A1, A2, B1, B2, C1, C2) caso usarmos a mesma estratégia teríamos que dizer que os dispositivos têm um grau de incerteza de “6 de símbolos". Acontece que essa não é a maneira como geralmente pensamos sobre informação e muito menos sobre como como acreditamos que ela deveria ser quantificada [1]. Como afirma Schneider:
“Por exemplo, se recebemos dois livros, nós preferíamos dizer que recebemos duas vezes a informação de um único livro.” [1]
Ou seja uma medida aditiva seria muito mais preferível. Felizmente, podemos obter este tipo de propriedade ao usarmos o logaritmo do número de símbolos possíveis. Este pequeno truque nos permite somar os logaritmos, ao invés da opção anterior que envolvia multiplicar o número de símbolos. Voltando ao exemplo de Schneider, o primeiro dispositivo nos deixaria em um estado de incerteza equivalente ao log(3), o segundo ao log(2) e os dois dispositivo combinados: log(3) + log(2) = log(6). Assim:
“A base do logaritmo determina as unidades. Quando usamos a base 2 as unidades estão em bits (base 10 nos dá 'digits', a dos logaritmos naturais, nos dá 'nats' [14] ou nits [15]). Assim, se um dispositivo produz um símbolo, temos a certeza de log2(1) = 0 bits, assim não temos incerteza sobre o que o dispositivo irá fazer em seguida. Se ele produz dois símbolos nossa incerteza seria log2(2) = 1 bit. Ao ler um mRNA, caso o ribossomo encontre qualquer uma das quatro bases igualmente prováveis, então a incerteza é de 2 bits.” [1]
Isso nos permite concluir que a fórmula para a incerteza é log2 (M)**. Aqui M refere-se ao número de símbolos. Esta fórmula pode ser também estendida para os casos em que os símbolos não são igualmente prováveis:
“Por exemplo, se existem 3 símbolos possíveis, mas um deles nunca aparece, então a nossa incerteza é de 1 bit. Se o terceiro símbolo aparece raramente, em relação aos outros dois símbolos, a nossa incerteza deve ser um pouco maior do que 1 bit, mas não tão elevada como log2 3 bits.” [1]
Podemos reorganizar a fórmula, o que nos deixa com:

de modo que P=1/M é simplesmente a probabilidade de qualquer símbolo aparecer.
É possível também generalizarmos esta equação para levarmos em contra as várias probabilidades dos símbolos Pi, de modo que as probabilidades somem 1 no total, o que equivale a 100% no jargão popular:
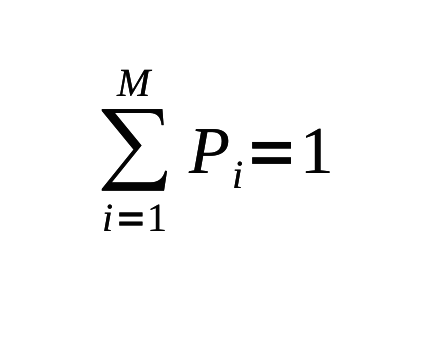
Lembrando aqui que o simbolo ∑ (SOMATÓRIO) significa que devemos adicionar todas as Pi, para todos i, começando em 1 e indo até M. A surpresa que temos quando observamos o iésimo tipo de símbolo foi chamada, “surpresa” (“surprisal”) por Tribus e é definida por analogia como sendo - log2P para ser

Assim, caso Pi aproxime-se de 0, ou seja, a probabilidade dele aparecer na mensagem seja muio baixa, ficaríamos muito surpresos ao descobrir o iésimo símbolo, uma vez que quase nunca ele deveria aparecer. Neste, caso, pela fórmula, ui aproxima-se do infinito, ∞. Em contraste, caso Pi =1, então, não haveria surpresa alguma ao nos deparamos com o iésimo símbolo, já que este símbolo deveria sempre aparecer, e, portanto, ui = 0. A incerteza, portanto, poder ser vista como a 'surpresa' média para uma sequência infinita de símbolos produzidas pelo dispositivo imaginado por Schneider [1].
A partir daí podemos encontrar a média para uma sequência de símbolos com N símbolos de comprimento que tenha um alfabeto formado por M símbolos. Caso suponhamos que o tipo do iésimo símbolo apareça Ni vezes, de modo que, se somarmos através de toda a cadeia e juntarmos os símbolos, isso seria o mesmo que somarmos através de todos os símbolos da cadeia, como podemos ver abaixo.
Desta maneira existirão Ni casos nos quais temos a surpresa ui e a surpresa média dos N símbolos será:
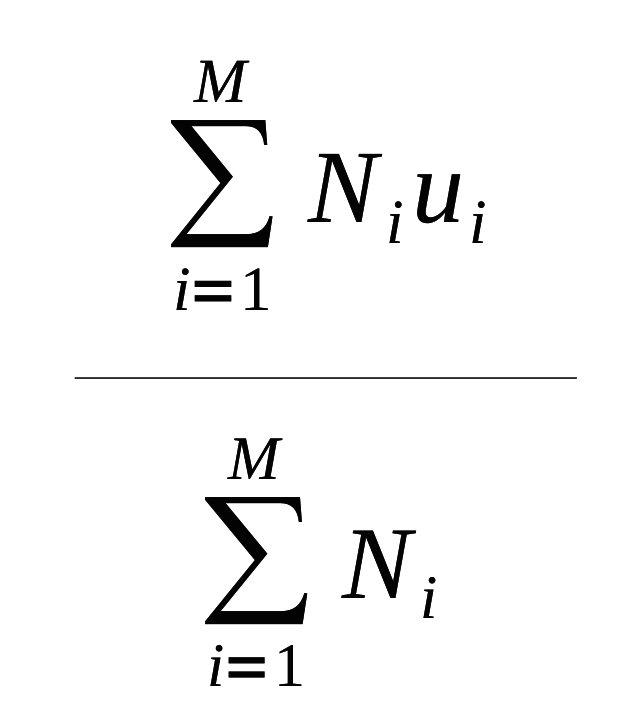
Substituindo N pelo denominador e trazendo-o para dentro do somatório de cima, obteremos:
Então, para uma sequência infinita de símbolos, a frequência Ni/N torna-se Pi, a probabilidade do iésimo símbolo. Fazendo essa substituição podemos notar que a nossa surpresa média (H) é:
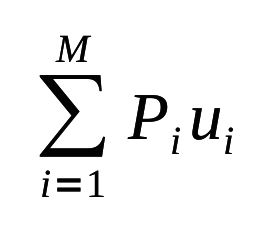
Finalmente, substituindo ui, obtemos a famosa fórmula geral de Shannon para a incerteza:

Como vimos bem no começo deste artigo (diferente dos exemplos de Schneider, como ele próprio deixa claro [1]), Shannon chegou a esta fórmula por um caminho muito mais rigoroso**** do que nós, ao postular várias propriedades desejáveis para a medida da incerteza, e só depois disso derivar a função. Ao lado podemos ver como se parece a função H no caso de apenas dois símbolos. Ali fica claro que a curva simétrica atinge seu máximo quando ambos os símbolos são igualmente prováveis, isto é Pi = 0.5) e cai para zero sempre que um dos símbolos torna-se dominante em detrimento do outro. Podemos ver isso com mais clareza ao seguirmos o exercício proposto por Schneider [1].
Comecemos supondo que todos os símbolos são igualmente prováveis. Isso quer dizer que Pi=1/M. Substituindo isso na equação da incerteza obtemos:
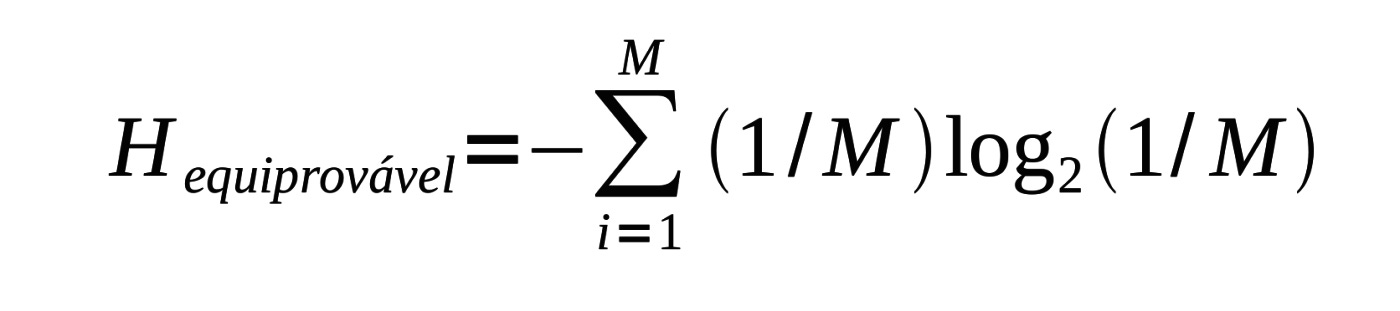
Uma vez que M não é uma função de i, podemos retirá-lo do somatório:
Fazendo isso acabamos com a mesma equação com a qual começamos. De acordo com Schneider, pode ser mostrado que para um determinado número de símbolos (ou seja, quando M é fixo) que a incerteza, H, tem seu maior valor somente quando os símbolos são igualmente prováveis. Por exemplo, uma 'moeda honesta' é mais difícil de prever os seus resultados (dos seus arremessos) do que uma 'moeda viciada' [1].
Mas e a informação do DNA?
Uma vez compreendidos esses conceitos mais fundamentais podemos dar um exemplo mais relevante, usando a biologia molecular, com o polímero biológico mais famoso, o DNA. Essa molécula é formada por cadeias de 4 tipos diferentes de nucleotídeos, portanto, M = 4:
A, C, G e T
Com probabilidades (Pi):
PA=½
PC=¼
PG=⅛
PT=⅛
As surpresas destas dos nucleotídeos equivalem a (-Log2Pi ):
uA=-Log2PA = -Log2PA(½)= 1 bit
uC=-Log2PC= -Log2PC(¼)= 2 bits
uG=-Log2PG= -Log2PG(⅛)= 3 bits
uT=-Log2PT= -Log2PT(⅛)= 3 bits
Neste casos a incerteza, H, é:

Mas o que significa dizer que um sinal tem 1,75 bits por símbolo?
Significa que podemos converter o sinal original em uma sequência de 1's e 0's (dígitos binários), de modo que, em média, existam 1,75 dígitos binários para cada símbolo no sinal original. Alguns símbolos terão mais dígitos binários (os mais raros) e outros terão menos (os mais comuns). Podemos recodificá-los para que o número de dígitos binários seja igual a 'surpresa' ( 'surprisal' ) [1]:

Desta forma, a cadeia ACATGAAC, cujas letras aparecem nas mesmas frequências que as probabilidades definidas anteriormente, podem ser codificadas como 10110010001101, onde 14 dígitos binários são utilizados para codificar oito símbolos, o que nos dá a média de 14/8 = 1,75 dígitos binários por símbolo (Schneider, 2006 e 2010) [2, 3]. Este é o chamado de “código de Fano” [1].
Esse tipo de código permite sua decodificação sem a necessidade de espaços entre os símbolos, mas, normalmente, é preciso saber o quadro de leitura, que neste exemplo pode ser facilmente descoberto. Isso acontece porque nesta forma de codificação em particular o primeiro dígito binário distingue entre o conjunto que contém A, (simbolizado por {A}) e o conjunto (C, G, T), que são, no conjunto, igualmente prováveis já que 1/2 = 1/4 + 1/8 + 1/8. O segundo dígito, usado caso o primeiro dígito seja 0, distingue C de G e T. O dígito final distingue G de T. Como cada escolha é tão provável como qualquer outra (na nossa definição original das probabilidades dos símbolos), cada dígito binário, neste código, carrega apenas 1 bit de informação [1].
Cuidado! Isso nem sempre será verdade. Um dígito binário fornece um bit apenas se os dois conjuntos representados pelos dígitos forem igualmente prováveis - como o caso aqui, pois o ajustamos deliberadamente o exemplo para que assim o fosse. Porém, nos casos que eles não sejam equiprováveis, cada dígito binário fornece menos de 1 bit, o que é óbvio pois a função H é máxima quando as probabilidades são as mesmas para todos os símbolos. (Schneider, 2006 e 2010) [2, 3].
Porém, como explica Schneider, não há nenhuma maneira de atribuir um código (finito) de modo que cada dígito binário tenha o valor de 1 bit, embora seja possível (ao empregar-se grandes blocos de símbolos) chegar mais perto deste ideal. No exemplo ajustado que acabamos de ver não há maneira de usar menos de 1,75 dígitos binários por símbolo, mas, nada impede que usemos mais e esbanjemos, usando dígitos extras para representar a mensagem. A medida da incerteza, H, portanto, nos diz o que é possível obter em uma situação ideal de codificação, o que automaticamente nos revela o que é impossível, ou seja, enviar a mensagem do exemplo com menos de 1,75 bits por símbolo, codificados utilizando-se apenas um dígito binário por símbolo (Schneider, 2010) [3].
Lembrando-nos que definimos informação como a redução da incerteza, agora, como temos uma fórmula geral para a incerteza, podemos começar a expressar a informação a partir dela.
Comecemos por imaginar que um computador contém alguma informação em sua memória. Então, caso fossemos vasculhar cada estado ligado-desligado*** - i.e. os equivalentes físicos das possibilidade binárias na memória do computador - teríamos uma incerteza de Hantes bits por estado ligado-desligado. Agora, porém, nós limpamos parte da memória do computador, definindo todos os valores como 'zero', ('desligados'), o que faz com que haja uma nova incerteza, menor do que o anterior: Hdepois*****.

Então, a memória do computador perdeu uma média de R= Hantes - Hdepois bits de informação por estado 'ligado-desligado'. Se o computador fosse completamente limpo, então Hdepois= 0 e R = Hantes.
Este ponto é muito importante. Muita confusão terminológica pode ser gerada caso isso não fique claro.
Agora vamos para outro exemplo. Desta vez, devemos pensar em uma antiga máquina de teletipo que recebe caracteres por meio de uma linha telefônica. Caso não houvesse qualquer ruído na linha telefônica e nenhuma outra fonte de erro existisse, o teletipo imprimiria o texto perfeitamente, sem qualquer erro. Porém, como existe ruído sempre haverá alguma incerteza em relação a se o caractere impresso é realmente o caractere que havia sido enviado. Portanto, antes de um caractere ser impresso, o teletipo deve estar preparado para qualquer um dos caracteres possíveis, e este estado tem a incerteza de Hantes . A questão é que mesmo após todos os caracteres tenham sido recebidos ainda há incerteza. É isso que Schneider chama de Hdepois. Esta incerteza é baseada na probabilidade de que o símbolo que foi recebido através da linha não seja igual ao símbolo que foi enviado e, portanto, mede a quantidade de ruído.
Por exemplo, imagine um sistema em que são transmitidos dois símbolos equiprováveis transmitidos a cada segundo a uma taxa de 1 bit por segundo sem erros. Agora, suponha que a probabilidade de que um '0' seja recebido quando um '0' é enviado é de 0,99, enquanto a probabilidade de que seja recebido um '1', quando de fato um '0' foi enviado, é de 0,01. No caso de ter sido enviado um '1', temos os mesmos valores, ou seja, 0,99 de ser recebido um '1' e por conseguinte 0,01 de ser recebido um '0'. Neste caso, a incerteza após o recebimento de um símbolo Hdepois= -0,99log20,99 - 0,01log20,01 = 0,081, de modo que a taxa real de transmissão, R = 1- 0,081=0,919 bits por segundo:
“Infelizmente muitas pessoas têm cometido erros porque não compreendem esse ponto claramente. Os erros ocorrem porque as pessoas assumem implicitamente que não há ruído na comunicação. Quando não há ruído, R = Hantes, como é o caso da memória de um computador sendo completamente apagada. Isto é, se não há ruído, a quantidade de informação transmitida é igual à incerteza antes da comunicação. Quando há ruído, e alguém assume que não há nenhum, isso leva a todos os tipos de filosofias confusas. Deve-se sempre levar em conta o ruído.” [1]
Nestas últimas décadas pesquisadores como Schneider vêm aplicando esta abordagem à biologia molecular, especialmente a evolução de biomoléculas, como as sequências de DNA e RNA e proteínas. No caso de Schneider, mais especificamente ao que alguns chamam de "máquinas moleculares" e a compreensão do como elas evoluíram nos seres vivos. Além de várias aplicações práticas na própria biologia molecular e biotecnologia, estes estudos servem de inspiração para o campo ainda mais amplo da nanotecnologia [2].
Aqui cabe destacar que a teoria da informação de Shannon aplicada a biologia molecular e a evolução não é uma mera curiosidade e nem uma tentativa desesperada de responder aos criacionistas. Existe um grande histórico da área e medida desenvolvida por Schneider baseada na teoria de Shannon tem mostrado-se tremendamente útil para caracterizar os padrões de sequências de DNA e RNA que definem os sistemas de controle genético [1, 2, 3]. De fato, Schneider mostrou que os sítios de ligação dos ácidos nucleicos (ou seja, aquelas sequências nas quais proteínas específicas ligam-se e modulam a ativação dos genes, alterando seus padrões de transcrição) geralmente contêm a quantidade certa de informação necessária para que os fatores de transcrição liguem-se a elas, encontrando-as no genoma [3]. Desta maneira, eventuais discrepâncias podem ser ainda mais ilustrativas. E exatamente isso que veremos nos próximos posts desta série. No próximo post vou me aprofundar mais um pouco no trabalho de Schneider e apresentar exemplos mais concretos do uso das medidas de R, Rsequência e Rfrequênciae sua relevância à biologia evolutiva. Por fim, apresentarei uma tradução de um vídeo criado pelo usuário cdk007 do youtube sobre a evolução da informação por meio da seleção natural de mutações aleatórias, inspirado em um trabalho de Schneider publicado em 2000 na revista Nuclear Acid Research, usando a teoria da informação molecular de Shannon e seu programa EV [4]. Até lá!
---------------------------------------------
* Existem várias medidas de informação, inclusive aplicadas à biologia, como explica Steve Frank em alguns artigos publicados na revista Journal of Evolutionary biology. Além disso, além de existirem precedentes a proposta por Shannon (inclusive nas quais o matemático americano se baseou para construir o seu trabalho a partir dos anos de 1940), existe uma outra versão bem conhecida da teoria da informação, a 'Teoria Algorítmica da Informação' (TAI), proposta e desenvolvida por vários autores diferentes, mas cujos principais nomes associados a ela são os dos matemáticos Andrei Kolmogorov e Gregory Chaitin. A TAI é outra abordagem ao problema da definição e quantificação da informação e sobre sua relação com a computação e com a aleatoriedade. Ela tem como base o conceito de 'complexidade algorítmica' (ou 'conteúdo informacional') de Kolmogorov que mede os recursos computacionais necessários para especificar uma dado objeto, como uma sequência de sinais, uma string - como em um texto, por exemplo. O conteúdo de informação ou a complexidade algorítmica de um objeto, neste sentido, pode ser medido pelo comprimento da sua descrição mais curta; ou, mais formalmente, como o 'comprimento do programa mais curto que calcula (ou gera como saída) o objeto em questão, sendo o programa executado em algum computador universal de referência fixo' [Hutter, 2008].
De acordo com Grunwald e Vitanyi (2008), tanto a versão da Teoria da Informação "clássica", de Shannon, como a Teoria Algorítmica da Informação partem da mesma ideia, isto é, que a informação (na verdade a função H) pode ser medida pelo número mínimo de bits necessários para descrever a observação. A diferença, segundo eles, é que, enquanto Shannon considera métodos de descrição dessa grandeza que são ideais em relação a alguma distribuição dada de probabilidade, a Teoria Algorítmica adota uma abordagem não probabilística, considerando qualquer programa de computador que primeiro calcule (imprima) a sequência que representa a observação e depois pare como sendo uma descrição válida. A quantidade de informação na sequência (string) é então definida como o tamanho (medido em bits) do programa mais curto de computador que gera a sequência e depois para. Isso implica que sequências regulares têm complexidade baixa, enquanto sequências aleatórias têm complexidade de Kolmogorov mais ou menos igual ao seu próprio comprimento, ou seja, uma sequência aleatória pode ser mais complexa do que uma sequência cheia de padrões. Isso pode também causar grande confusão, remetendo de novo ao alerta de Schneider sobre o uso mais técnico do termo informação e o perigo da equiparação de informação à incerteza e à entropia.
Segundo Chaitin, a TAI é "o resultado de colocar a teoria da informação de Shannon e teoria da computabilidade de Turing em uma coqueteleira e agitando vigorosamente." [via wikipedia]. A TAI também sofre abusos por parte dos criacionistas, mas desta vez é o conceito de complexidade (que tem uma definição formal bem rigorosa) que é o alvo. Devo, em outra oportunidade, explorar algumas abordagens à biologia molecular e à evolução que empregam mais esta teoria.
Frank, S. A. Natural selection. V. How to read the fundamental equations of evolutionary change in terms of information theory. Journal of Evolutionary Biology 25:2377-2396. doi:10.1111/jeb.12010
Frank, S. A. Natural selection maximizes Fisher information. Journal of Evolutionary Biology 22:231-244. doi:10.1111/j.1420-9101.2008.01647.x
Grunwald, Peter D.; Vitanyi, Paul M. B. (2008) Algorithmic information theory ARXIV eprint arXiv:0809.2754 2008arXiv0809.2754G.
Hutter, Marcus (2008), Algorithmic complexity Scholarpedia, 3(1):2573. doi:10.4249/scholarpedia.2573
**Também é possível usar outras bases de logaritmo, como fazem outros grupos de pesquisadores, como veremos em outro post desta série, como é o caso dos trabalhos de Christof Adami e Charles Ofria que empregam como base dos logaritmos o número de monômeros das macromoléculas de interesse (20 para os aminoácidos e 4 para os ácidos nucleicos). Porém, por enquanto, usaremos a base 2 o que nos permite quantificar a informação em termos de Bits.
***Schneider adota o termo "flip-flop” que eu preferi chamar de 'ligado-desligado' para evitar o uso da palavra "bit" enquanto discute a codificação de Fano já que há dois significados para essa palavra:
1. Um dígito binário, 0 ou 1. Só podendo ser um inteiro. Estes "bits" são as partes individuais dos dados dos computadores.
2. Uma medida de incerteza, H ou R. Esta informação pode ser qualquer número real porque é uma média. É a medida que Shannon utilizado para discutir sistemas de comunicação.
****O objetivo de Shannon era desenvolver uma forma de quantificar a informação associada a uma mensagem de modo que quanto mais improvável fosse a mensagem maior seria a informação ganha pelo receptor. Portanto, dado um conjunto de mensagens X no qual X = {x1,x2, x3,... xk}, uma distribuição de probabilidades do tipo P [X], isto é, P = {P1, P2, P3,... Pk} em que a probabilidade pi = P(xi) para cada mensagem xi. Lembrando que pi deve ser maior ou igual a zero ( pi ≥ 0) e a soma total deve ser igual a 1 ( p1 + p2+...+ pk = 1), já que não existem probabilidades menores que 0 e nem maiores que 1 (ou 100%).
Para conseguir alcançar este objetivo, Shannon precisava de uma fórmula bem específica, uma vez que uma medida da incerteza na comunicação de X teria que exibir uma série de características que mais ou menos já vinham sendo investigadas e postuladas por vários outros matemáticos e cientistas; devendo ser uma função com um valor real, (1) H(X), ou seja, H(X) teria que uma distribuição de probabilidade de X, tal que P[X] → R; (2) contínua [H(p1, ..., pk)], (3) aditiva [H (p1q1, ..., pkqk) = H(P) + H(Q) para as distribuições de probabilidade P e Q]; (4) monotônica [ou seja, deveria aumentar com k para distribuições uniformes: If l > k, então H(Q) > H(P) para qualquer P = (1/k, ..., 1/k) e Q = (1/l, ..., 1/l); além de ser (5) 'ramificada', isto é, H(p1,..., pk) deveria ser independente de como o processo é dividido em partes, e, por fim, (6) deveria ser normalizável em bits, onde o ganho médio de informação para duas mensagens igualmente prováveis seria 1 bit: H(1/2, 1/2) = 1.
De acordo com Shannon existiria uma única função que teria todas estas propriedades e que poderia quantificar a tal 'entropia informacional' ou seja, o valor esperado médio de uma distribuição de probabilidade P:
H(X ) = −∑ pi log pi
H(X) é máxima quando p1 = p2 = ... = pk = 1/k, isto é quando a distribuição de probabilidade é uniforme e as probabilidades são equiprováveis.
H(X) = 0 apenas quando a probabilidade de xi (pi ) é 1 e todas as outras são 0.
O logaritmo usado é de base 2: logx = y ⇒ x = 2y, o que permite a quantificação em bits.
*****Shannon usou a notação Hy(x), ou seja, a incerteza condicional do receptor y dada a mensagem enviada a partir de x, para o que chamamos de Hdepois, que, por sinal, ele também chamou de "equivocação" [1].
----------------------------------------------------------------
Referências:
Schneider, Thomas D. Information Theory Primer With an Appendix on Logarithms version = 2.65 of primer.tex 2012 Mar 14 [PDF]
Schneider TD. A brief review of molecular information theory. Nano Commun Netw. 2010 Sep;1(3):173-180. doi: 10.1016/j.nancom.2010.09.002
Schneider TD. Claude Shannon: biologist. The founder of information theory used biology to formulate the channel capacity. IEEE Eng Med Biol Mag. 2006 Jan-Feb;25(1):30-3.
Schneider TD. Evolution of biological information. Nucleic Acids Res. 2000 Jul 15;28(14):2794-9. doi: 10.1093/nar/28.14.2794